알고리즘에 대해

 

알고리즘이란

입력값을 출력값의 형태로 바꾸기 위해 어떤 명령들이 수행되어야 하는지에 대한 규칙들의 순서적 나열 이다.

정확하고 효율적인 알고리즘

알고리즘의 평가할 때는 정확성도 중요하지만, 효율성도 중요합니다.
효율성은 작업을 완료하기까지 얼마나 시간과 노력을 덜 들일 수 있는지에 대한 것입니다.

코딩 알고리즘은 다음과 같은 요소로 구성됩니다:

1. 이해 및 분석: 먼저 주어진 문제를 이해하고 분석하여 어떤 입력이 주어졌을 때 어떤 결과를 원하는지 파악합니다.
2. 알고리즘 설계: 문제 해결을 위한 알고리즘을 설계합니다. 이 단계에서는 주어진 문제에 대한 해결 방법을 결정하고 그에 따른 절차를 계획합니다.
3. 알고리즘 구현: 설계한 알고리즘을 실제 코드로 구현합니다. 이 단계에서는 선택한 프로그래밍 언어를 사용하여 알고리즘을 구현하고 테스트합니다.
4. 평가 및 개선: 구현된 알고리즘을 평가하고 성능을 개선하기 위해 필요한 조치를 취합니다. 이 단계에서는 알고리즘이 예상대로 작동하는지 확인하고 필요에 따라 수정합니다.

"n", "n/2", "log n" 등은 알고리즘의 시간 복잡도를 나타내는 표기법입니다. 이러한 표기법은 알고리즘의 성능을 분석하고 비교하는 데 사용됩니다.

1. n: "n"은 입력 크기를 나타냅니다. 즉, 알고리즘에 입력되는 데이터의 크기입니다. 예를 들어, 배열의 길이가 "n"이라면 배열에 저장된 요소의 개수가 입력 크기가 됩니다.
2. n/2: "n/2"는 입력 크기의 절반을 나타냅니다. 이것은 주로 배열이나 리스트와 같은 자료구조에서 반복문이나 분할 작업을 수행할 때 사용됩니다. 예를 들어, 배열의 원소를 반으로 나누는 경우에 "n/2"를 사용할 수 있습니다.
3. log n: "log n"은 로그 함수를 의미하며, 일반적으로는 밑이 2인 로그를 가리킵니다. 이는 입력 크기에 대한 로그 시간복잡도를 나타냅니다. 이 표기법은 주로 이진 검색과 같은 분할 정복 알고리즘에서 사용됩니다. "log n"의 값이 작을수록 입력 크기에 대한 알고리즘의 성능이 좋습니다.

알고리즘의 시간복잡도

 

 

 

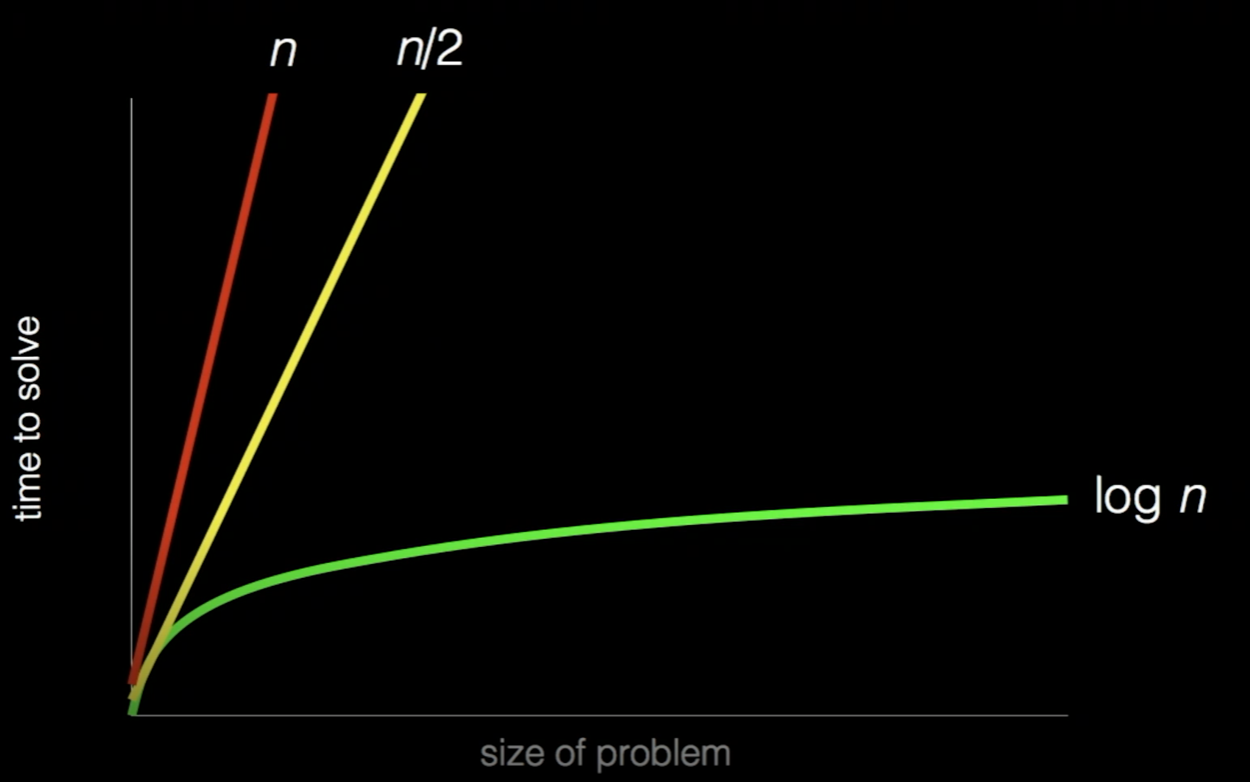
시간복잡도

앞서 이야기했던 효율적인 알고리즘을 구현한다는 것은 바꾸어 말해 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 구성했다는 이야기입니다.

위의 두 가지 경우에서 첫번째 알고리즘은 페이지가 늘어나는 만큼 같은 비율으로 해결하는 시간이 증가합니다. 이게 시간복잡도 N
하지만, 두번째 알고리즘은 100페이지가 늘어나더라도 한 번의 절차만 더 수행하면 되므로 늘어난 문제에 비해 해결시간은 거의 미미하게 증가합니다. 이게 시간복잡도 log n